三角形

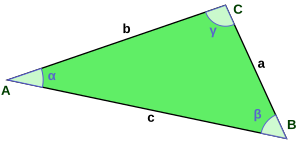
三角形，幾何之初义也，蓋三線段相接所成者。其線段曰邊，其交曰點，二邊於形內交處所成之角曰內角。

大寫

A

、

B

、

C

諸文，今慣以名三角形之頂點；於厥邊也，則以小寫

a

、

b

、

c

諸文。角則或

\alpha

、

\beta

、

\gamma

，或復用點名。

平面幾何纂

內角和恆為二直角，故無多於一直角者。

有一直角者，曰勾股，今謂直角三角形。《九章算術》劉徽注曰：“短面曰勾，長面曰股，相與結角曰弦”。直角兩旁，短者曰勾，長者曰股，直角相對者曰弦。

有一鈍角者，謂鈍角三角形。若三角均為銳角，謂銳角三角形。

又有殊者，即二或三角相等也。若二角相等，所對邊等長，謂等腰三角形；若三角皆等，則三邊皆等長，謂等邊三角形。

知三邊長，則知其三角；知二邊長及其夾角，可得未知邊長。是以三角形穩固甚，故用於支架之物，多作三角形。

知三內角，則知其三邊比例，反以亦然。若兩三角形內角相同，曰相似三角形也。

有球面幾何，內角和可大于二直角；有雙曲幾何，內角可小于二直角。窮究其理，所謂「內角和恆為二直角」，等價於平行公理也。

流形之學，有三角化之術。三角形者，二單體也，意其三點之凸組合也。