併集

註︰蓋當今數學之事，誠難僅以文述，而無符號，故凡數學之文，咸有漢字、拉丁字相易之事，以合文言、數學，則無論文理之人，皆可明之也。

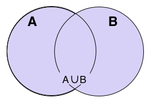
併集者，合二集也，港台之人謂之曰「聯集」。

A 與 B 之併集

定義

收二集之元素，并歸一集，謂之併集（記曰「 $A\cup B$」）。

併集術曰︰「若有集，則其元素之併集亦存。」

例

• 奇偶之集相合，可得整數之集耳。
• 「金、木、土」之集，并「水、火、土」之集，得五行之集。（記曰「 {金,木,土} U {水,火,土}={金,木,水,火,土} 」）
• 凡不足一而逾零者，并而得一集；不足二而逾一者，亦得一集；不足三而逾二者，亦得一集。如是復計，則得無窮集。此無窮集相併，正數之集是也。（記曰「${(x\mid 0\leq x\leq 1)}\cup {(x\mid 1\leq x\leq 2)}\cup {(x\mid 2\leq x\leq 3)}\cup ...={(x\mid x\geq 0)}$」）
• 集自并，亦為己耳。（記曰「$A\cup A=A$」）

參

• 交集

集論

元素｜ 集｜ 族｜ 子集｜ 交集｜ 併集｜ 補集｜ 冪集｜ 有序對｜ 直積｜ 關係｜ 映射｜ 等價｜ 偏序